How to Read Network Attributes in R

março 06, 2022 Postar um comentário

Network Analysis with R | Manipulating Network Data

Perform network analysis and manipulate network data with igraph in R.

Introduction

Network analysis is a technique that uses graph theory to study complex real-globe issues, such every bit computational biology, technology, finance, marketing, neuroscience, political science, and public wellness (Kolaczyk et al., 2014). In my previous works, I have done quite a lot of network analysis in the python environment with NetworkX and node2vec. Still, recently I came beyond the book - "Statistical Analysis of Network Data with R" (this is the 1st version, and the 2d version was published in 2020)- written by Eric D. Kolaczyk and Gábor Csárdi, which showed me many cool packages (e.g., igraph) in R which provides high-quality network analysis in terms of manipulating graphs, mathematical modeling, statistical modeling, etc.

The volume came with a list of lawmaking demos, which can exist constitute here: https://github.com/kolaczyk/sand.

This blog is congenital upon Affiliate 2 of the book: Manipulating Network Data, assuming that y'all already understood the basic concepts of network analysis, such as nodes, edges, etc. Notwithstanding, if you demand a comprehensive explanation, I encourage you lot to read the book.

What you need:

RStudio (or similar IDEs) and "igraph" (an R parcel, available in CRAN)

In case you practice non have "igraph" installed:

                      ## Download and install the bundle            
install.packages("igraph")                                ## Load package            
library(igraph)

Code

Create Undirected and Directed Graphs

To manually create a graph, the function "graph.formula" tin be used.

To make information technology more than understandable for creating directed graphs, I proposed an airport network consisting of three airports: JFK (New York City airport), PEK (Beijing airdrome), and CDG (Paris airdrome). Thus, the directed graph that I created tin be read: we only take ane-fashion flights from JFK to PEK and CDG (presume some travel restrictions applied); PEK and CDG are mutually continued, and yous can fly both ways.

Become Basic Info of the Graphs

To brand the blog concise, the balance of the demo will only focus on undirected graphs. For more than reference, please visit the book'southward GitHub repository.

A graph, represented past G = (5, E), is a mathematical construction consisting of a set V of vertices and a set Eastward of edges. The number of vertices and the number of edges in the graph are sometimes called the social club and size of graph Chiliad (Kolaczyk et al., 2014).

You may use V(graph) and E(graph) to cheque the vertices and edges; use vcount(graph) and ecount(graph) to check the lodge and size of the graph; employ print_all(graph) to show the summary of the graph.

Visualize the graph

Y'all may utilize the command of plot(graph) to visualize the graph:

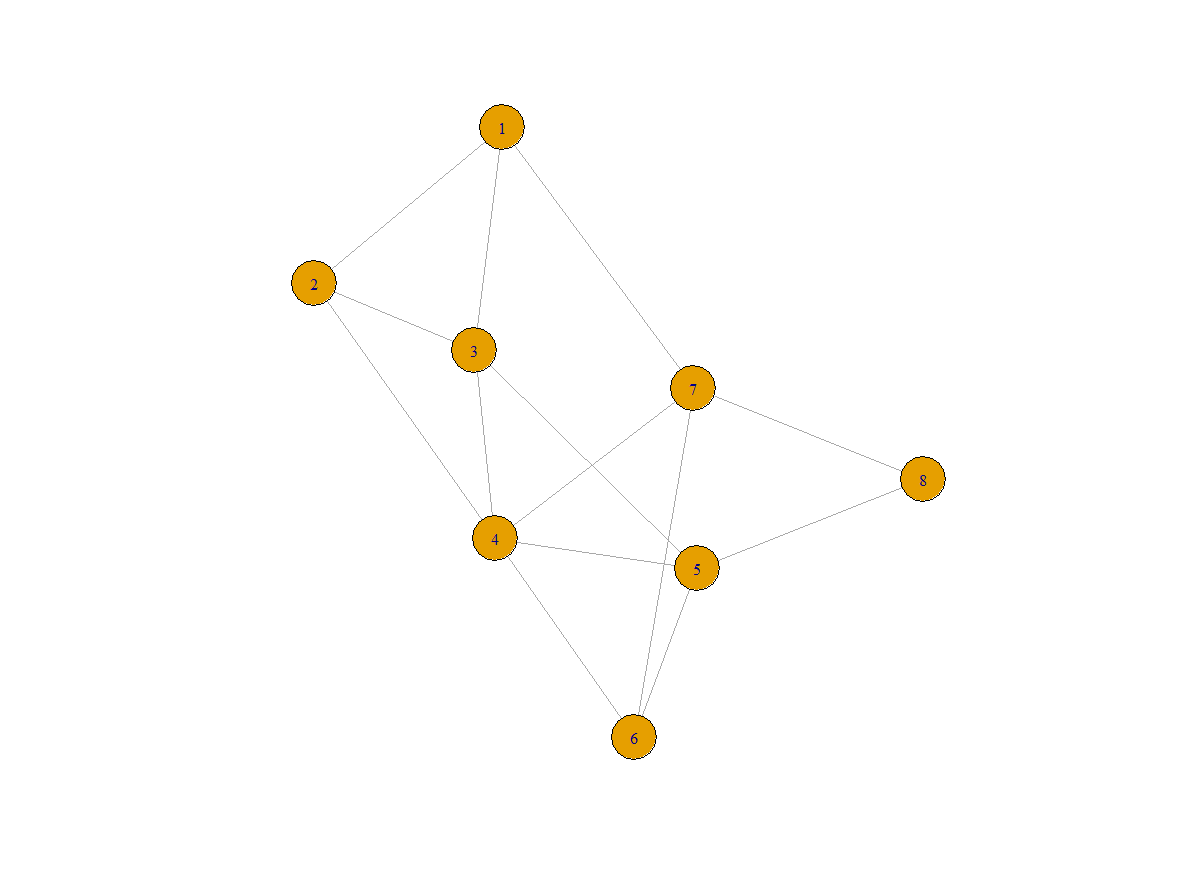
Label the vertices

I fabricated the graph whose vertices were labeled with numbers i through N. In practise, you might already have natural labels, such equally names. So here is how you could label your vertices and how information technology would look like:

          5(one thousand)$proper name <-c("Adam","Judy","Bobby","Sam","Frank","Jay","Tom","Jerry")          plot(g)

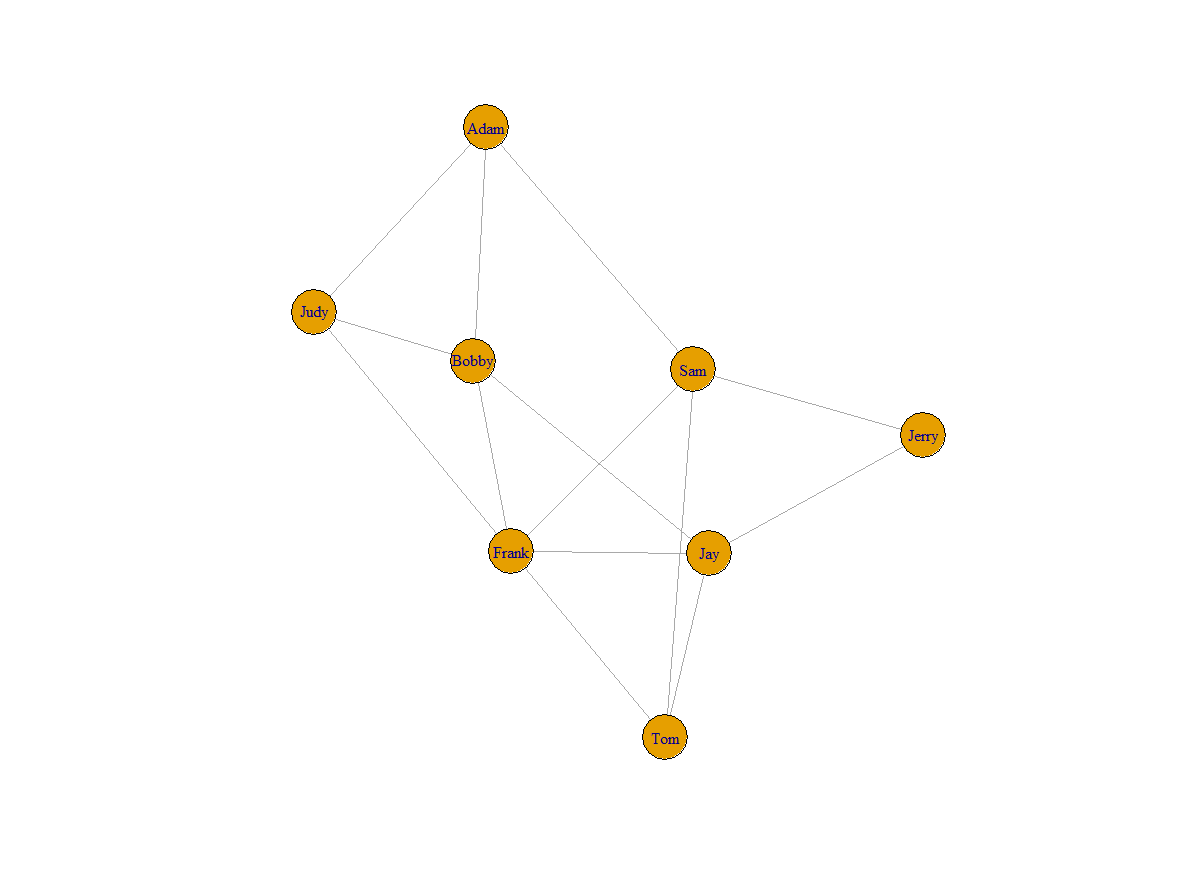
Representations for Graphs

Normally, the graph will be stored in 3 basic formats: adjacency lists, edge lists, and adjacency matrix (Kolaczyk et al., 2014).

An adjacency list is a drove of unordered lists. Each unordered list describes the prepare of neighbors of a specific vertex in the graph within an adjacency listing. This format is what igraph uses in the graph summary function.

An edge list is a two-column table to list all the node pairs in the graph. This format is preferred by NetworkX (in python).

The adjacency matrix's entries bear witness whether ii vertices in the graph are continued or not. If there is a link between two nodes, "i and j," the row-cavalcade indices (i, j) will be marked equally 1, otherwise 0. Therefore, the adjacency matrix will exist symmetric for undirected graphs. Statistical models normally prefer to encode graphs with this format, such as node2vec which requires the adjacency matrix every bit inputs.

You tin use the functions of get.adjlist(graph) , get.edgelist(graph) , and become.adjacency(graph) to get the 3 different formats, respectively.

Operations on Graphs

In practice, we might want to remove sure edges or join graphs to go subgraphs. In this example, the math operators tin can assistance yous achieve the goal.

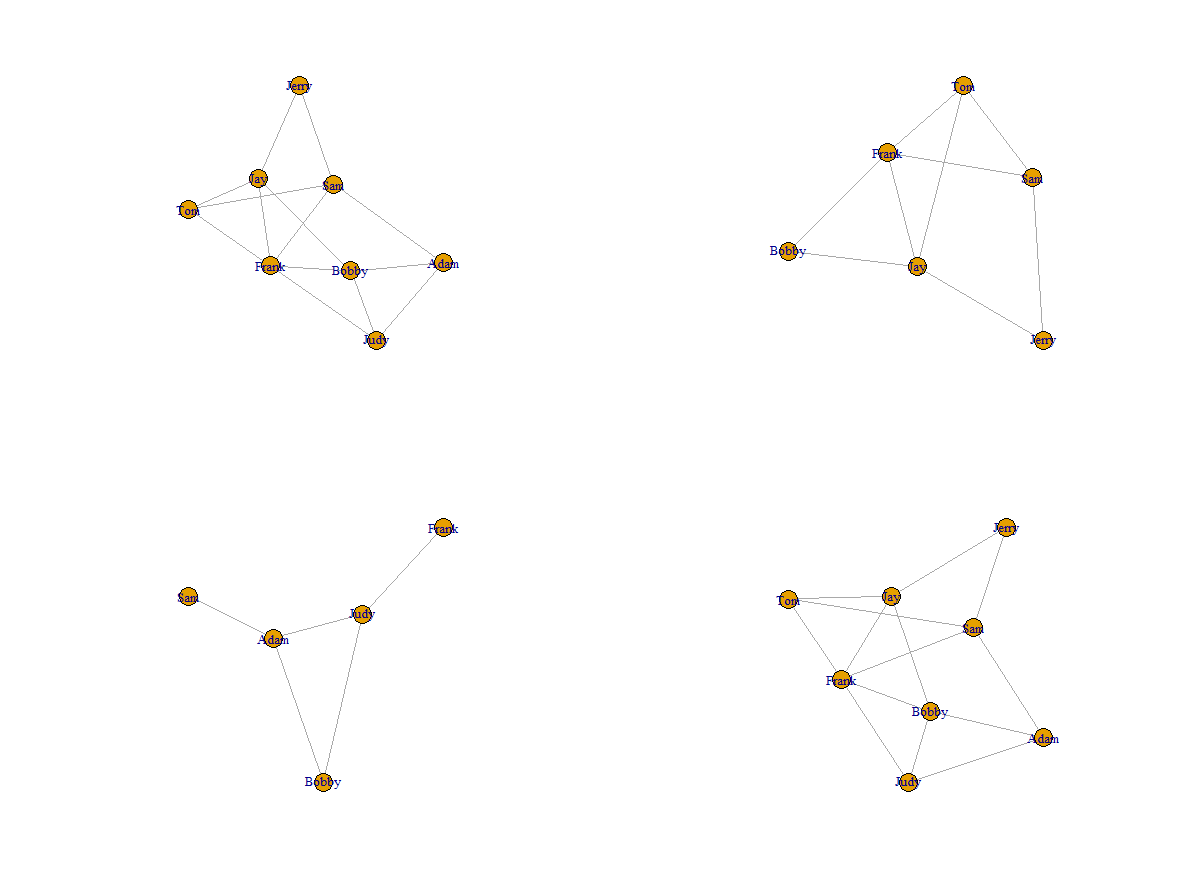
The graph in (1, 1) is the original graph. The graph in (1, 1) removed two vertices from the original graph. The graph in (2, 1) is made of sure edges (the edges were removed from the original graph due to the removal of vertices). The graph in (2, 2) is the joined graph of (1, 1) and (two, 1), and it has the same construction as (1, one).

Using Data Frames

In real-world problems, we rarely make graphs manually. Instead, nosotros have to import information. For the best do to dispense graphs, we unremarkably need to set up two data files/data frames. 1 of the files needs to comprise all the attributes for each vertex in the graph. The other file needs to incorporate the edges in the network (typically an edge list).

In the book, the author gave an example of a lawyer dataset of Lazega. The information is stored in two different files: elist.lazega and v.attr.lazega . The original data is available in the sand (Statistical Analysis of Network Data) library. Therefore, hither is how yous would read your own data:

Decision

In this blog, I covered the code for creating directed and undirected graphs, visualizing graphs, getting statistics from graphs, labeling vertices, generating different formats of representations, subsetting and joining graphs, and reading your own network data with igraph.

Reference

Statistical Assay of Network Data with R, by Eric D. Kolaczyk and Csárdi Gábor, Springer, 2014, pp. xiii–28.

johnswoperand1967.blogspot.com

Source: https://towardsdatascience.com/network-analysis-in-r-manipulating-network-data-ee388fba7215

Johns Woperand1967